در دنیای پیچیده ریاضیات، دو مفهوم کلیدی به نامهای “مشتق” و “انتگرال” هستند که به مانند دو ابزار قدرتمند، برای تحلیل و درک تغییرات و الگوهای پنهان در طبیعت و فناوری به کار میروند. از محاسبه سرعت حرکت یک خودرو تا مدلسازی رشد جمعیت، این دو مبحث بنیادی در قلب بسیاری از علوم و مهندسیها قرار دارند. در این مقاله، ما به بررسی این مفاهیم شگفتانگیز خواهیم پرداخت و شما را با اهمیت و کاربردهای گستردهی آنها آشنا خواهیم ساخت. تا انتهای مقاله با برنا اندیشان همراه باشید و به دنیای جذاب مشتق و انتگرال قدم بگذارید.
مقدمهای بر مشتق و انتگرال
مشتق و انتگرال از مفاهیم بنیادین ریاضیات هستند که در بسیاری از رشتههای فنی، مهندسی، و علوم پایه، نقش کلیدی دارند. این دو مبحث، که به ترتیب مربوط به تغییرات لحظهای و مساحت زیر منحنیها هستند، درک عمیق و تسلط بر آنها میتواند برای موفقیت در بسیاری از دروس دانشگاهی و حتی در آزمونهای مختلف ضروری باشد.
در این مقاله، به طور مفصل به توضیح مفاهیم مشتق و انتگرال خواهیم پرداخت، کاربردهای آنها را بررسی میکنیم و در نهایت، به معرفی دوره آموزشی جامع خانم مریم داورپناه خواهیم پرداخت که به صورت ویژه به آموزش این مفاهیم پرداخته است.
مشتق چیست؟
مشتق یک تابع، بیانگر نرخ تغییرات آن تابع در هر نقطه از دامنهاش است. به عبارتی دیگر، مشتق نشان میدهد که چگونه خروجی یک تابع نسبت به تغییرات ورودی آن تغییر میکند. این مفهوم یکی از ارکان مهم حساب دیفرانسیل است و برای مدلسازی تغییرات در بسیاری از حوزهها از جمله فیزیک، اقتصاد و مهندسی کاربرد دارد.
مفهوم هندسی مشتق
از نظر هندسی، مشتق یک تابع در یک نقطه، شیب خط مماس به منحنی آن تابع در آن نقطه است. این خط نشاندهنده سرعت تغییرات تابع در آن لحظه خاص است. به طور مثال، در فیزیک، مشتق مسافت نسبت به زمان، همان سرعت را نشان میدهد.
کاربردهای مشتق
مشتق در بسیاری از مسائل علمی و مهندسی کاربرد دارد. از جمله مهمترین کاربردهای آن میتوان به موارد زیر اشاره کرد:
1. محاسبه سرعت و شتاب: در فیزیک، مشتقهای مکان به زمان، سرعت و شتاب را تعیین میکنند.
2. بهینهسازی: مشتق در پیدا کردن نقاط بهینه (حداقل و حداکثر) یک تابع کاربرد دارد که در مسائل مختلف از جمله اقتصاد و مهندسی بسیار مهم است.
3. مدلسازی تغییرات اقتصادی: برای تحلیل نرخ تغییرات قیمتها، هزینهها یا درآمدها از مشتق استفاده میشود.
انتگرال چیست؟
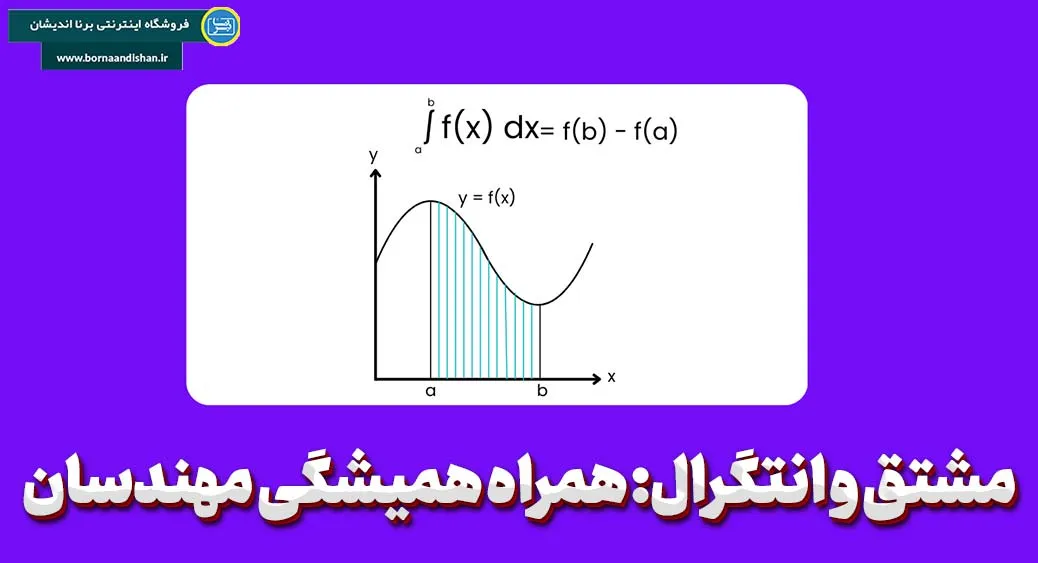
انتگرال معکوس مشتق است. به عبارت سادهتر، انتگرال به محاسبه مساحت زیر یک منحنی میپردازد. اگر مشتق به ما نرخ تغییرات یک تابع را بدهد، انتگرال به ما مقدار تجمعی آن تغییرات را از یک نقطه به نقطه دیگر میدهد. انتگرال به دو نوع تقسیم میشود: انتگرال معین و انتگرال نامعین.
مفهوم هندسی انتگرال
هندسی انتگرال به معنای محاسبه مساحت زیر منحنی تابع از یک نقطه خاص تا نقطه دیگر است. برای مثال، اگر بخواهیم مساحت زیر منحنی یک تابع را بین دو نقطه خاص محاسبه کنیم، از انتگرال معین استفاده میکنیم.
کاربردهای انتگرال
انتگرال نیز همانند مشتق در بسیاری از مسائل علمی و مهندسی کاربردهای وسیعی دارد. برخی از مهمترین کاربردهای آن عبارتند از:
1. محاسبه مساحت و حجم: برای محاسبه مساحتهای پیچیده و یا حجم اجسام سهبعدی از انتگرال استفاده میشود.
2. محاسبه کار و انرژی: در فیزیک، محاسبه کار انجام شده توسط یک نیرو یا انرژی ذخیره شده در یک سیستم با استفاده از انتگرال انجام میشود.
3. مدلسازی فرآیندهای پیوسته: در بسیاری از فرآیندهای طبیعی و مهندسی که تغییرات پیوسته دارند، از انتگرال برای مدلسازی و تحلیل استفاده میشود.
تعریف انتگرال ناسره
انتگرال ناسره به آن دسته از انتگرالها اطلاق میشود که در آنها دامنه انتگرال یا تابع انتگرال به گونهای است که نمیتوان به روشهای معمول آنها را محاسبه کرد. این انتگرالها معمولاً نیاز به روشهای ویژهای دارند که از طریق آنها میتوان به جواب رسید.
انواع انتگرالهای ناسره
انتگرالهای ناسره ممکن است به دلیل وجود انفجار در تابع یا مرزهای بینهایت در دامنه انتگرال بوجود آیند. برای مثال، اگر تابعی در یک نقطه خاص به بینهایت میل کند یا دامنه انتگرال بینهایت باشد، انتگرال آن به صورت ناسره در نظر گرفته میشود.
کاربردهای انتگرال ناسره
انتگرالهای ناسره در مسائل فیزیکی و مهندسی مانند تحلیل سیگنالها، پخش گرما و مسائل مربوط به مکانیک آماری کاربرد دارند. به عنوان مثال، در فیزیک، گاهی اوقات برای محاسبه اثرات ناشی از نیروهای نقطهای که به بینهایت میل میکنند، از انتگرالهای ناسره استفاده میشود.
ارتباط مشتق و انتگرال
مشتق و انتگرال به طور عمیقی به یکدیگر وابسته هستند. این دو مفهوم در واقع دو جنبه مختلف از تغییرات یک تابع را بیان میکنند. در حالی که مشتق نرخ تغییرات یک تابع را نشان میدهد، انتگرال مجموع تغییرات را از یک نقطه به نقطه دیگر محاسبه میکند.
یکی از اصول مهم ریاضی که این ارتباط را مشخص میکند، قضیه اساسی حساب دیفرانسیل و انتگرال است. طبق این قضیه، اگر یک تابع پیوسته باشد، انتگرال آن میتواند به عنوان معکوس مشتق آن تابع در نظر گرفته شود.
اهمیت آموزش مشتق و انتگرال در رشتههای فنی و مهندسی
برای دانشجویان رشتههای فنی و مهندسی، تسلط بر مباحث مشتق و انتگرال نه تنها در درسهای ریاضی عمومی یک و دو الزامی است، بلکه در دروس تخصصیتر مانند معادلات دیفرانسیل، دینامیک، تحلیل ساختارها و بسیاری دیگر از دروس پیشرفته، به عنوان پیشنیاز ضروری است. بنابراین، آموزش دقیق و جامع این مفاهیم برای موفقیت در این رشتهها بسیار حیاتی است.
معرفی پکیج آموزشی “مشتق و انتگرال” خانم مریم داورپناه
اگر شما نیز به دنبال یادگیری جامع و عمیق مباحث مشتق و انتگرال هستید، پکیج آموزشی خانم مریم داورپناه یک انتخاب عالی برای شماست. این دوره به طور کامل به آموزش مفاهیم مشتق، کاربردهای آن، انتگرال، کاربردهای انتگرال و انتگرال ناسره پرداخته و میتواند نیاز دانشجویان رشتههای فنی – مهندسی و علوم پایه را به طور کامل برآورده کند.
ویژگیهای دوره آموزش
پوشش جامع سرفصلها: تمامی مباحث مشتق و انتگرال به طور کامل، از تعاریف تا کاربردهای پیشرفته بررسی میشود.
مثالها و تمرینهای متنوع: این آموزش شامل مثالها و تمرینهایی است که به شما کمک میکند تا مفاهیم را به طور کامل درک کنید و در امتحانات موفق شوید.
آموزش به شیوهای ساده و روان: با توجه به تجربه تدریس خانم مریم داورپناه در دانشگاهها و مؤسسات آموزشی مختلف، این دوره به گونهای طراحی شده که پیچیدگیها به زبان ساده و روان بیان شود.
پیشنیازها: در این دوره فرض بر این است که شما با مفاهیم حد و پیوستگی آشنا هستید و با توابع مختلفی مثل توابع مثلثاتی و نمایی آشنایی دارید.
در نهایت، با استفاده از کد تخفیف cdemada، میتوانید این پکیج آموزشی را با قیمت استثنایی تهیه کنید. برای دریافت اطلاعات بیشتر و تهیه دوره، کافی است به لینک زیر مراجعه فرمایید.
دوره آموزشی جامع مشتق و انتگرال خانم مریم داورپناه، با تدریس کامل و جامع مباحث مرتبط، به شما کمک میکند تا در دروس ریاضی عمومی یک، معادلات دیفرانسیل و دیگر دروس تخصصی مهندسی و علوم پایه، موفقیت چشمگیری کسب کنید.
سخن آخر
در پایان این مقاله، خوشحالیم که تا اینجا با برنا اندیشان همراه بودید و در دنیای جذاب مشتق و انتگرال قدم گذاشتید. امیدواریم توانسته باشیم مفاهیم پیچیده را به سادهترین و بهترین شکل ممکن برای شما توضیح دهیم. یادگیری ریاضیات، مسیر پرچالشی است، اما با آموزشهای درست و منابع مناسب، میتوانید به تسلط کامل برسید. از همراهی شما سپاسگزاریم و امیدواریم که با استفاده از پکیجهای آموزشی برنا اندیشان، قدمهای بزرگی در راه موفقیت علمیتان بردارید.