تبدیل لاپلاس، ابزاری قدرتمند در دنیای ریاضیات و مهندسی است که میتواند پیچیدگیهای معادلات دیفرانسیل را به فرمولهایی قابل حل تبدیل کند. این مبحث، با کاربردهای گستردهای که در رشتههای مختلف دارد، میتواند گام مهمی در تسلط بر مفاهیم پیشرفته باشد. تا انتهای این مقاله با برنا اندیشان همراه باشید تا با مفاهیم این تبدیل و کاربردهای آن آشنا شوید و قدم به قدم از دنیای پیچیده معادلات دیفرانسیل به دنیای سادهتر و قابل فهمتر وارد شوید.
مقدمهای بر تبدیل لاپلاس
تبدیل لاپلاس یکی از ابزارهای ریاضی بسیار کاربردی است که در بسیاری از رشتههای علوم پایه، مهندسی و فنی، به ویژه در معادلات دیفرانسیل، کاربرد دارد. این تبدیل به طور ویژه برای حل معادلات دیفرانسیل خطی با ضرایب ثابت و غیرثابت، بسیار مفید است. در این مقاله، به بررسی کامل تبدیل لاپلاس و کاربردهای آن در حل معادلات دیفرانسیل، از جمله معادلات انتگرالی و دستگاههای معادلات دیفرانسیل خواهیم پرداخت. این ابزار ریاضی میتواند پیچیدگیهای معادلات دیفرانسیل را به یک مسئله سادهتر تبدیل کرده و فرایند حل را تسهیل کند.
مفهوم تبدیل لاپلاس
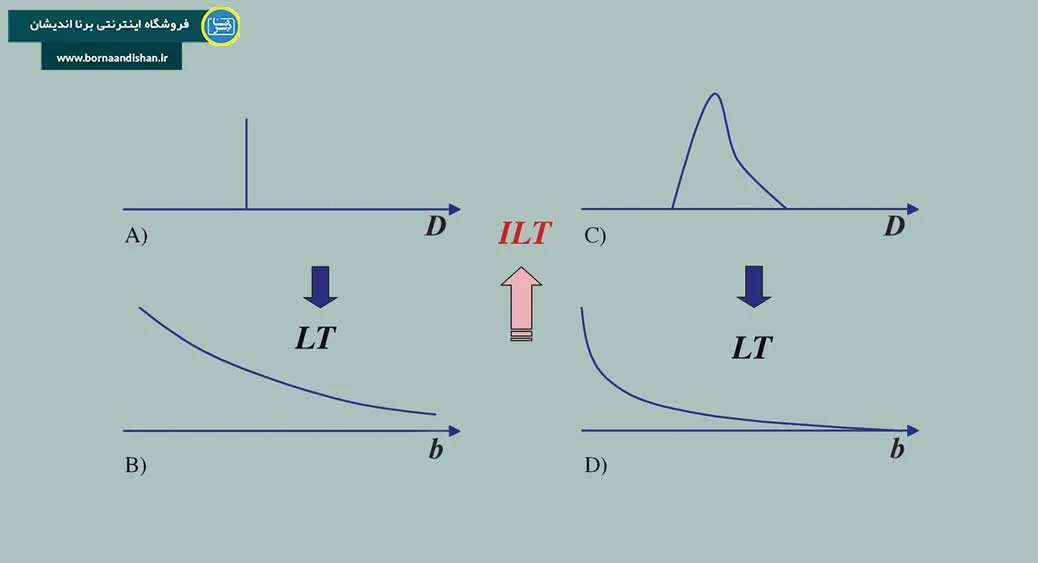
تبدیل لاپلاس یک ابزار جبری است که یک تابع زمانی را به یک تابع پیچیدهتری به نام تابع لاپلاس تبدیل میکند. این تبدیل به نام ریاضیدان فرانسوی پییر سیمون لاپلاس نامگذاری شده است و برای حل مسائل پیچیده در مهندسی، فیزیک، و ریاضیات استفاده میشود. هدف اصلی تبدیل لاپلاس تبدیل یک معادله دیفرانسیل پیچیده به یک معادله جبر ساده است که میتوان آن را به راحتی حل کرد و سپس نتیجه را با استفاده از تبدیل معکوس لاپلاس به حالت اولیه بازگرداند.
تبدیل لاپلاس در واقع یک فرآیند انتقال از دنیای زمان به دنیای فرکانس است. این ویژگی به خصوص در حل معادلات دیفرانسیل که در آنها مشتقات زمان یا متغیرهای پیچیده وجود دارند، بسیار موثر است. با استفاده از تبدیل لاپلاس، میتوان معادلات دیفرانسیل را به معادلات جبری تبدیل کرده که حل آنها نسبت به معادلات دیفرانسیل اصلی سادهتر است.
تبدیل لاپلاس در حل معادلات دیفرانسیل
در بسیاری از مسائل مهندسی و فیزیک، معادلات دیفرانسیل بهعنوان ابزار اصلی برای مدلسازی پدیدهها و سیستمها استفاده میشوند. این معادلات معمولاً در قالب معادلات غیرخطی یا پیچیده هستند و حل آنها ممکن است بسیار دشوار باشد. تبدیل لاپلاس یکی از روشهایی است که میتواند به سادهتر کردن حل این معادلات کمک کند.
بهطور مثال، در مسائل مربوط به مدارهای الکتریکی، مکانیک، و کنترل، معادلات دیفرانسیل اغلب در توصیف رفتار سیستمها ظاهر میشوند. تبدیل لاپلاس این معادلات را به فرمهایی تبدیل میکند که بهراحتی میتوان آنها را حل کرده و سپس نتیجه را به حالت زمانی بازگرداند.
کاربردهای تبدیل لاپلاس
1. حل معادلات دیفرانسیل خطی: یکی از مهمترین کاربردهای تبدیل لاپلاس در حل معادلات دیفرانسیل خطی با ضرایب ثابت است. بهطور معمول، حل چنین معادلاتی با استفاده از روشهای کلاسیک مشکل است، اما با تبدیل آنها به فضای لاپلاس، معادلات به فرمولهای جبری تبدیل میشوند که به راحتی قابل حل هستند.
2. حل معادلات دیفرانسیل غیرخطی: برخی از معادلات دیفرانسیل غیرخطی نیز میتوانند با استفاده از تبدیل لاپلاس سادهتر شوند. البته این نوع مسائل ممکن است نیاز به استفاده از تکنیکهای خاصی داشته باشند.
3. مدلسازی سیستمهای فیزیکی و مهندسی: سیستمهای فیزیکی مانند مدارهای الکتریکی، ارتعاشات مکانیکی، و سیستمهای کنترل معمولاً بهوسیله معادلات دیفرانسیل توصیف میشوند. با استفاده از تبدیل لاپلاس، میتوان رفتار این سیستمها را تحلیل کرد.
4. حل معادلات انتگرالی: تبدیل لاپلاس همچنین در حل معادلات انتگرالی مفید است. این نوع معادلات معمولاً در تحلیل سیستمها و پدیدههای طبیعی به کار میروند و با استفاده از تبدیل لاپلاس میتوان به سادگی آنها را حل کرد.
معکوس تبدیل لاپلاس
یکی از مفاهیم مهم در تبدیل لاپلاس، معکوس آن است. زمانی که یک معادله دیفرانسیل را بهوسیله تبدیل لاپلاس به یک معادله جبری تبدیل میکنیم، نتیجهای که بهدست میآید، در فضای لاپلاس است. اما برای بازگشت به حالت اولیه و دریافت جواب معادله در دنیای واقعی، باید از معکوس تبدیل لاپلاس استفاده کنیم.
روشهای مختلفی برای پیدا کردن معکوس تبدیل لاپلاس وجود دارند. یکی از روشهای معمول، استفاده از جدول تبدیلهای لاپلاس است که شامل تبدیلها و معکوسهای معمول و شناخته شده است. علاوه بر آن، میتوان از روشهای انتگرالی نیز برای محاسبه معکوسهای پیچیدهتر استفاده کرد.
ویژگیها و مزایای استفاده از تبدیل لاپلاس
1. کاهش پیچیدگیهای ریاضی: تبدیل لاپلاس بهطور چشمگیری پیچیدگی معادلات دیفرانسیل را کاهش میدهد و آنها را به معادلات جبری تبدیل میکند که حل آنها سادهتر است.
2. قابلیت حل معادلات با شرایط اولیه: تبدیل لاپلاس بهطور خاص برای حل معادلات دیفرانسیل با شرایط اولیه مفید است. این ویژگی باعث میشود که تبدیل لاپلاس به ابزاری ایدهآل برای تحلیل سیستمهای دینامیکی تبدیل شود.
3. کاربرد گسترده در علوم مختلف: تبدیل لاپلاس تنها محدود به معادلات دیفرانسیل نیست بلکه در بسیاری از رشتههای دیگر مانند فیزیک، مهندسی، آمار، و اقتصاد نیز کاربرد دارد.
4. حل مشکلات در دنیای فرکانسی: بسیاری از مسائل در دنیای فرکانسی راحتتر قابل تحلیل و حل هستند. تبدیل لاپلاس میتواند به تحلیل مشکلات در این فضا کمک کند.
دوره آموزشی معادلات دیفرانسیل توسط خانم مریم داورپناه
اگر شما نیز علاقهمند به یادگیری جامع و کامل مباحث مرتبط با تبدیل لاپلاس و کاربرد آن در معادلات دیفرانسیل هستید، پیشنهاد میکنم دوره آموزشی خانم مریم داورپناه را که بهطور ویژه برای تدریس این مفاهیم طراحی شده است، تهیه کنید. خانم داورپناه با بیش از دو دهه تجربه تدریس در دانشگاههای معتبر و مؤسسات آموزشی، دورهای جامع و کامل در زمینه معادلات دیفرانسیل و تبدیل لاپلاس ارائه دادهاند که میتواند به شما در تسلط بر این مبحث کمک شایانی کند.
این دوره شامل ۱۶۶ مسئله حل شده است که به شما کمک میکند تا درک عمیقتری از مباحث مختلف پیدا کنید. همچنین، روش تدریس ساده و شیوا، همراه با ارائه مثالهای فراوان و آزمونهای تشریحی، باعث میشود تا شما بهراحتی با مسائل و پیچیدگیهای معادلات دیفرانسیل و تبدیل لاپلاس آشنا شوید.
دوره آموزش تبدیل لاپلاس و معادلات دیفرانسیل خانم مریم داورپناه در آکادمی نیکدرس منتشر شده است و میتوانید با مراجعه به لینک زیر، این دوره مفید را تهیه کنید و به یادگیری این مبحث مهم بپردازید.
شما عزیزان میتوانید با استفاده از کد تخفیف cdemada، پکیج آموزش جامع و کامل تبدیل لاپلاس خانم مریم داورپناه را با قیمت استثنایی تهیه فرمایید! این دورهی آموزشی با تدریس یکی از مجربترین اساتید دانشگاهی، به شما این امکان را میدهد که بهصورت حرفهای و دقیق مباحث پیچیدهی تبدیل لاپلاس را در معادلات دیفرانسیل یاد بگیرید.
این فرصت عالی را از دست ندهید و هماکنون با وارد کردن کد تخفیف cdemada، به بهترین قیمت ممکن دسترسی پیدا کنید. برای شروع یادگیری و تسلط بر این مبحث پرکاربرد، کافیست به لینک زیر مراجعه کنید و پکیج آموزشی خود را با تخفیف ویژه تهیه کنید.
نتیجهگیری
در این مقاله، به بررسی مفهوم تبدیل لاپلاس، کاربردهای آن در حل معادلات دیفرانسیل و ویژگیهای آن پرداخته شد. تبدیل لاپلاس ابزاری قدرتمند در حل معادلات دیفرانسیل است که میتواند بهطور چشمگیری پیچیدگیهای مسائل را کاهش دهد. یادگیری کامل این مبحث میتواند به شما در درک بهتر مفاهیم پیشرفته ریاضی و فیزیک کمک کند. همچنین دوره آموزشی خانم مریم داورپناه، بهعنوان یک منبع جامع و کامل، میتواند به شما کمک کند تا تسلط کامل بر این مبحث پیدا کنید.
سخن آخر
در پایان، از شما عزیزان که تا انتهای این مقاله با برنا اندیشان همراه بودید، صمیمانه تشکر میکنیم. امیدواریم که مطالب ارائه شده برای شما مفید و کاربردی بوده باشد و توانسته باشیم شما را در مسیر یادگیری و تسلط بر مفاهیم پیچیده تبدیل لاپلاس یاری کنیم. همیشه در کنار شما خواهیم بود تا با هم به موفقیتهای بزرگتری دست یابیم.